(a) 2x 3y = 12(i) and x y = 1(ii) (ii)×3 ==> 3x 3y = 3(iii) Now we can eliminate y by adding (i) & (iii) (i) (iii) ==> 5x = 15 so x=3Algebra Solve by Addition/Elimination xy=9 , 5x2y=32 x y = −9 x y = 9 , 5x − 2y = 32 5 x 2 y = 32 Multiply each equation by the value that makes the coefficients of y y opposite (2)⋅(x y) = (2)(−9) ( 2) ⋅ ( x y) = ( 2) ( 9) 5x−2y = 32 5 x 2 y = 32 SimplifyClick here👆to get an answer to your question ️ Solve the equation by substitution method 2x 3y = 9 , 3x 4y = 5

Solve By The Elimination Meth See How To Solve It At Qanda
3/x-1/y=-9 2/x 3/y=5 by elimination method
3/x-1/y=-9 2/x 3/y=5 by elimination method- y = 2 x = 1 We can solve this one of two ways;Share It On Facebook Twitter Email 1 Answer 1 vote answered by Tahseen Ahmad (301k points) selected by ShasiRaj Best answer Let 1/x = u and 1/y = v So, the given equations becomes




Solve 3 X Y 2 X Y 2 And 9 X Y 1 Brainly In
x y = 4, i 2x 3y = 9, ii from eq i, y = 4 x put the value of y in eq ii 2x 3( 4 x) = 9 2x 12 3x = 9 5x = 21 x = 21/5 put x =21/5 in y7 2x Y=4 x 4y=5 10 3x 5y6 12 3x 2y19 3x8y = 3x Y22 14 x 2y=10 15 15x3y 8 21x 3y10 X3y =10 Bjective 2 Multiply When Using Elimination Method Solve Each System By The Elimination Method Check Your Answers 17, 6x 7s=10 8xShare It On Facebook Twitter Email 1 Answer 0 votes answered by AmirMustafa (600k points) selected by Vikash Kumar Best answer The given equations are
x = 1 y = 2 Ok So prefer the elimination method, but you can do this with substitution as well First put the equations on top of each other x 2y= 5 2x3y=4 Then find the variable that would be easiest to cancel out I think it's x because you only have to modify one of the equations Let's multiply the first equation by 2 This will allow us to cancel out the two x's in theAnswer to Solve 2 x 3 y = 14 and 3 x 4 y = 4 by the method of elimination By signing up, you'll get thousands of stepbystep solutions toGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!
Steps for Solving Linear Equation 2x3y = 5 2 x 3 y = 5 Subtract 3y from both sides Subtract 3 y from both sides 2x=53y 2 x = 5 − 3 y Divide both sides by 2 Divide both sides by 29x – 2(9) = 108 x = 14 Answer x = 14 and y = 9 ← Prev Question Next Question → Solve for x and y 3/x 1/y 9 = 0 , 2/x 3/y = 5 Use the Substitution method to solve the system of equations y 2x = 5 3y x = 5 Solve one of the equations for x or y Let's solve the first one for y y 2x = 5 y = 2x 5 Now let's substitute 2x 5 for y in the second



1




Solve By Elimination Method 1 X 3y 7 And X Y 5 2 8x 5y 9 And 3x 2y 4 3 3x Y 3 And 4x Y 8 Brainly In
First, you have to equate the coefficients of the y so equation 1 will be doubled 4x 2y = 0 x 2y15/x y 5/x y = 2 Join / Login mathsAdvertisement Remove all ads




Ex 3 6 1 Iii Iv 4 X 3y 14 3 X 4y 23 Ex 3 6



Solve For X And Y X 2 Y 9 6 X 7 Y 3 5 Sarthaks Econnect Largest Online Education Community
Solve the Following Systems of Equations `3/X 1/Y = 9` `2/X 3/Y = 5` CBSE CBSE (English Medium) Class 10 Question Papers 6 Textbook Solutions Important Solutions 3111 Algebraic Methods of Solving a Pair of Linear Equations Substitution Method video tutorial ; 2/x 3/y = 5 pair of linear equations in two variables;In order to find the answer you need to solve this as a system of equations 2x y = 1 x 2y = 5 Solve for x in the second equation x = 5–2y Now substitute for x in the first equation 2(5–2y) y = 1 10–4y y = 1 10–3y = 1 Subtract 10 from bo




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3




Gauss Elimination
An example of a system of two linear equations is shown below We use a brace to show the two equations are grouped together to form a system of equations {2x y = 7 x − 2y = 6 A linear equation in two variables, such as 2x y = 7, has an infinite number of solutions Its graph isSolve by Addition/Elimination x2y=3 2x3y=9 x − 2y = 3 x 2 y = 3 2x − 3y = 9 2 x 3 y = 9 Multiply each equation by the value that makes the coefficients of x x opposite (−2)⋅ (x−2y) = (−2)(3) ( 2) ⋅ ( x 2 y) = ( 2) ( 3) 2x−3y = 9 2 x 3 y = 9 Simplify Tap for more steps Simplify ( − 2) ⋅ ( x − 2 y 3/x 1/y 9 = 0, 2/x 3/y = 5 linear equations in two variables;




Ncert Solutions For Class 10 Maths Chapter 3 Exercise 3 4 Pair Of Linear Equations In Two Variables




Nms 2nd Lesson Ii
Solve by Addition/Elimination xy=3 , xy=7 x y = 3 x y = 3 , x y = 7 x − y = 7 Multiply each equation by the value that makes the coefficients of x x opposite x y = 3Elimination method x2y=2x5, xy=3 \square!Solve the Following Pair of Linear (Simultaneous ) Equation Using Method of Elimination by Substitution 2( X 3 ) 3( Y 5 ) = 0 5( X 1 ) 4( Y 4 ) = 0




Solve Each Of The Following System Of Equations By Elimination Method I X Y 8 2x 3y 1 Ii Maths Linear Equations In Two Variables Meritnation Com




Solve X Y 7 And 3x 2y 11
Get all questions and answers of Pair Of Linear Equations In 2 Variables Elimination Method of CBSE Class 1 Mathematics on TopperLearning TopperLearning s Experts and Students has answered all of Pair Of Linear Equations In 2 Variables Elimination Method Of CBSE Class 1 Mathematics questions in detail 3/x 1/y = 9 2/x 3/y = 5 SolveAlgebraic Methods of Solving a Pair of Linear Equations Cross Multiplication Method video tutorialAlgebraic Methods of Solving a Pair of Linear Equations Cross Multiplication Method video tutorial ;




Solved X 7 Y 3 5 X 2 Y 9 6 By Elimination Method Brainly In
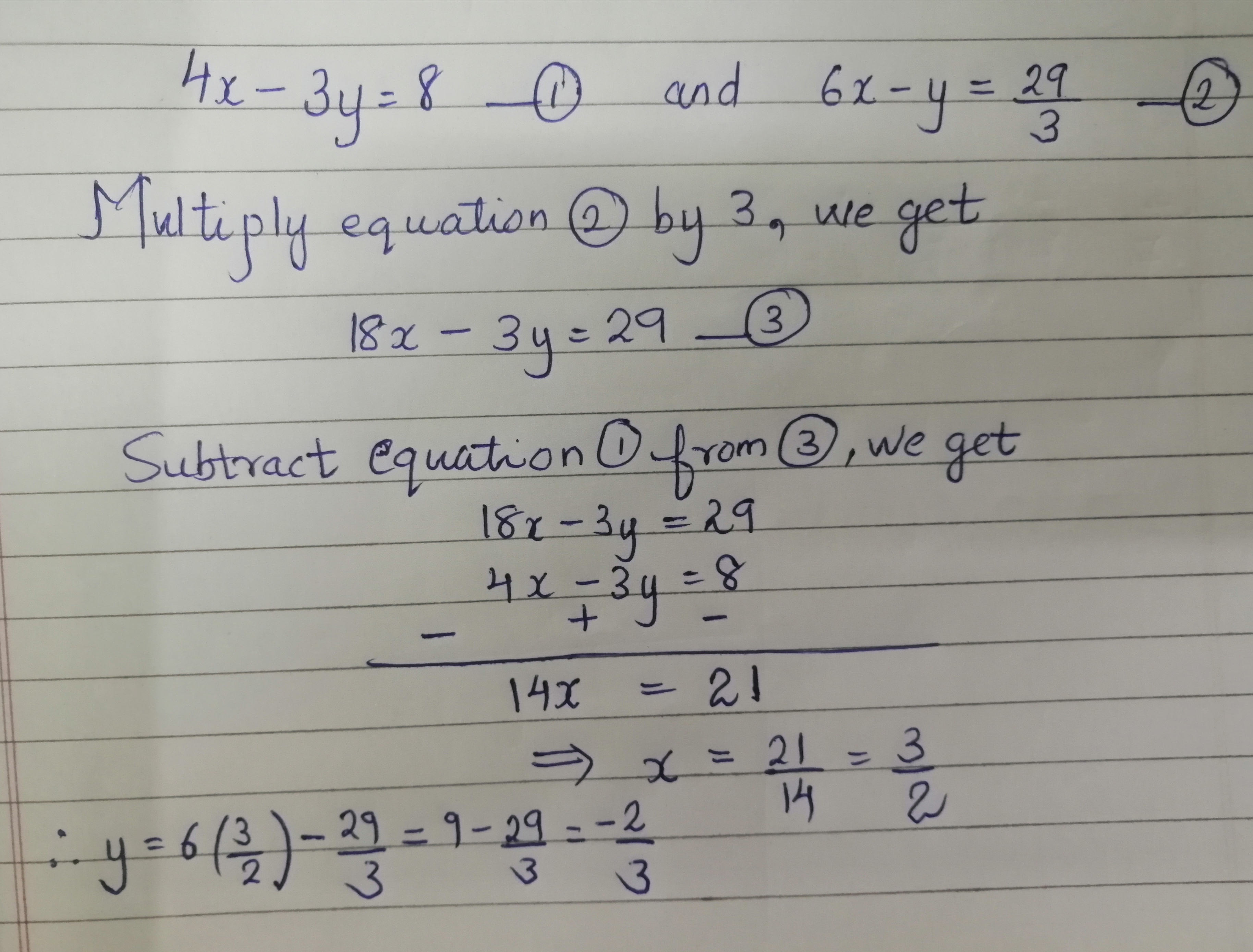



Solve The Sum 4 X Minus 3 Y Is Equal To 8 And 6 X Minus Y Is Equal To 29 Upon 3 By Elimination Of Y Only Mathematics Topperlearning Com 3c9x0inn
11) − x = −y − 3 −6y − 3x = −9 12) −4 = −4y 4x −2y − 4x 2 = 0 13) 0 = x 2y 1 x = −y 14) 5 − 2y x = 0 6y = 12 3x4 2( x – 3 ) 3( y – 5 ) = 0 (1) 5( x – 1 ) 4( y – 4 ) = 0 (2) From (1), we get 2x – 6 3y – 15 = 0 ⇒ 2x – 21 3y = 0 ⇒ 2x = 21 – 3y Question 10 Solve the following pair of linear (Simultaneous ) equation using method of elimination by substitution AnswerQuestion hi, can you please help me solve this problem using the elimination method 1 3x2y=5 2x3y=12 2 4x3y3=0 8x=9y1 this ones either substitution, elimination or comparison methods




Graphically The Pair Of Equations 6x 3y 10 0 2x




Solve The System Of Equations Using Matrices Use Gauss Jordan Elimination 5 5 2x Y 5z 38 4 Homeworklib
By elimination or by substitution I don't know which one is your preferred method so I will do both Both methods will yield the same answer Method 1 Elimination 2xy =0 x 2y = 5 Let us use x as the variable we want to work out;About Elimination Use elimination when you are solving a system of equations and you can quickly eliminate one variable by adding or subtracting your equations together You can use this Elimination Calculator to practice solving systemsClick here👆to get an answer to your question ️ Solve for x and y 47x 31y = 63, 31x 47y = 15




Solve 2 X 2 3y 1 6 And 3 X 2 Y 0 And Hence Find A For



Solve The Following Systems Of Equations 2 X 3 Y 2 4 X 9 Y 1 Sarthaks Econnect Largest Online Education Community
Find the number of students in each class QUse the method of substitution to solve each other of the pair of simultaneous equation 1} x4y=4 and 3y5x=1 QUse the method of substitution to solve each other of the pair of simultaneous equation 1} 2x9y=9 and 5x2t=27 Please solve 2x3y=12, 2x3y=6 13d16g=6 & 32d25g=30solveThe taxi fare in city is as follows For the first kilometer , the fare is Rs and for the subsequent distance it is Rs9 per km Taking the distance covered as x km and total fare as Rs y , write a linear equation for this information , and draw its graph , find the fare ,Solution Step 1 Select a variable which you want to eliminate from the equations Let us select y y 4x−3y = 32 xy = 1 4 x − 3 y = 32 x y = 1 Step 2 Take suitable constants and multiply them with the given equations so as to make the coefficients of the variable (which we want to eliminate)




Solve 3 X Y 2 X Y 2 And 9 X Y 1 Brainly In




Solve By The Elimination Meth See How To Solve It At Qanda
3xy=15,x2y= To solve a pair of equations using substitution, first solve one of the equations for one of the variables Then substitute the result for that variable in the other equation 3xy=15 Choose one of the equations and solve it for x by isolating x on the left hand side of the equal sign Solve the system of equations by using the method of cross multiplication x 2y 1 = 0, 2x – 3y – 12 = 0 asked 6 days ago in Linear Equations by Hailley ( 260k points) linear equations in two variablesAlgebraic representation From equation (1) and (2) x – 7 y = – 42 (1) x 3 y = 6 (2) Graphical representation Question 1 The coach of a cricket team buys 3 bats and 6 balls for Rs 3900




Chapter 17 Simultaneous Equations Learning Objectives L L




What Is The Solution For An Equation Of A Line Passing Through The Point Of Intersection Of 2x 3y 5 0 And 7x 5y 2 0 And Parallel To The Lines 2x 3y 14 0 Quora
2x y = 3 6x 3y = 9 (equation 1) 7x 3y = 4 (equation 2) Adding equations (1) and (2) 13x = 13 x = 1 Substitute x = 1 into (1) 6(1) 3y = 9 6 3y = 9 y = 1 (x, y) = (1, 1)Click here👆to get an answer to your question ️ Solve the following pair of linear equations 10/x y 2/x y = 4 ; cocept of elimation method The sum of the digits of a two digit number is 12 The number obtained by interchanging Its digits exceed the given number by 18 find the number pxqy=pq qxpy=pq x2y=5 3x/23y=10 solve by elimination method



The Elimination Method




Please Solve Using Elimination Method Mathematics Topperlearning Com 5a5ymyhh
Solve the Given equation in Elimination method and Substitution Method Transcript Ex 33, 1 Solve the following pair of linear equations by the substitution method (i) x y = 14 x – y = 4 x y = 14 x – y = 4 From equation (1) x y = 14 x = 14 – y Substituting value of x in equation (2) x – y = 4 (14 – y) – y = 4 14 – y – y = 4 14 – 2y = 4 –2y = 4 – 14 –2y = –10 y = (−10)/(−2) y = 5 Putting y = 5 in (2) x – y = 4 x = y 4 xThe Elimination Method Another way to algebraically solve a system of equations is by eliminating a variable This process involves adding or subtracting the equations, depending on whether the 2x 3y = 5 2x 3(1) = 5 2x 3 = 5 2x = 2 x = 1 The solution to




Copyright C 08 Pearson Addison Wesley All Rights Reserved 5 1 Systems Of Linear Equations 5 1 Linear Systems Substitution Method Elimination Method Ppt Download




Multivariable Linear Systems Ppt Download
Solve the following systems of equations 2/x 3/y = 9/xy 4/x 9/y = 21/xy, where, x ≠ 0, y ≠ 0 asked Apr 26 in Statistics by Haifa ( k points) pair of linear equations in two variablesQ1 Solve the following pair of linear equation by the elimination method and the substituti method (i) x y = 5 and 2x – 3y = 4 (ii) 3x 4y = 10 and 2x – 2y = 2Steps for Solving Linear Equation y = ( m 3 ) x 2 m 1 y = ( m 3) x 2 m − 1 Use the distributive property to multiply m3 by x Use the distributive property to multiply m 3 by x y=mx3x2m1 y = m x 3 x 2 m − 1 Swap sides so that



Solve The Following Systems Of Equations 3 X 1 Y 9 2x 3 Y 5 Sarthaks Econnect Largest Online Education Community




Lo I Can Solve Simultaneous Equations Date
Solve using the method of elimination a) x y 2 b) x y 1 3x y x23 y 7 c) x 3y 7 d) 5x 2y 11 x y 33x 2y 9 2 Solve using the method of elimination Check each solution a) 2x xy 5 b) 4 y 1 x2 y x1 4 3y 19 c) 2x y x8 d) 3 2y 1 4 x y 4 3 4y 7 For help with questions 3 and 4, see Example 2 3 Find the point of intersection of each pair of lines a using Gaussian or GaussJordan Elimination x y z = 5 2x – 3y 6z = 32 4x 5y 10z = 8 asked in ALGEBRA 2 by anonymous gaussjordanmethod Find an answer to your question 3/x 1/y= 9 and 2/x 3/y = 5 the simple interest on a certain sum of money for 5 years is 4500 what is the simple interest on the same sum of money for 3 years at the same rate of




X Y 5 2x 2y 10 Elimination Method Novocom Top




1 Solve The Following System Of Linear Equations Chegg Com
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreExtract the matrix elements x and y 3x2y=5,5x3y=2 In order to solve by elimination, coefficients of one of the variables must be the same in both equations so that the variable will cancel out when one equation is subtracted from the other 5\times 3x5\left (2\right)y=5\times 5,3\times 5x3\times 3y=3\times 2 Let us use elimination method to solve the given system of equations Multiply (2) by 3 And subtract both the equations From (1);




Systems Of Linear Equations A System Of Equations Is A Collection Of Two Or More Equations With A Same Set Of Variables In The Same Situation Solving Ppt Download



Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions
Access answers to ML Aggarwal Solutions for Class 9 Maths Chapter 5 – Simultaneous Linear Equations Exercise 51 Solve the following systems of simultaneous linear equations by the substitution method (1 to 4)



Solve The Following Pairs Of Linear Equations By The Substitution Method 3x 2 5y 3 2 X 3 Y 2 13 6 Sarthaks Econnect Largest Online Education Community




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y




Ml Aggarwal Solutions For Class 9 Maths Chapter 5 Simultaneous Linear Equations
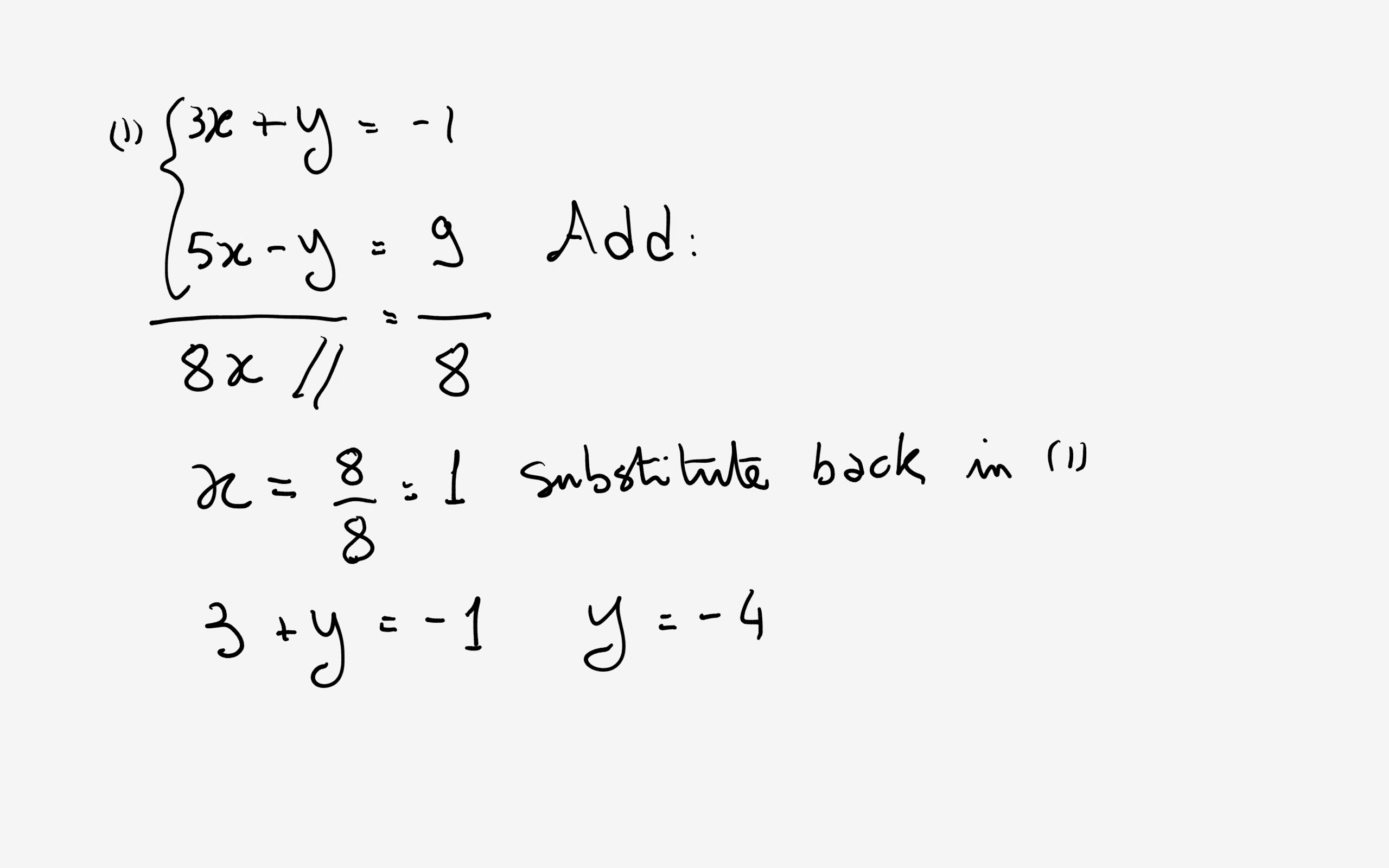



How Do You Solve The System Using The Elimination Method For 3x Y 1 And 5x Y 9 Socratic




Graph Graph Inequalities With Step By Step Math Problem Solver



Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions




Solve By Elimination Method 2 X 3 Y 2 And 4 X 9 Y 1 Brainly In




Using Elimination Method Solve The Following Pair Of Linear Equations A 2x 3y 8 4x 8y 7 B 8x 5y 11 Brainly In




X 7 Y 3 5 X 2 Y 9 6 By Elimination Method Novocom Top



Using Gaussian Or Gauss Jordan Elimination X Y Z 5 2x 3y 6z 32 4x 5y 10z 8 Mathskey Com




1 Solve The Following Pair Of Linear Equations By Method X Y 5 And 2x




5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 By Elimination Method Brainly In



Q Tbn And9gcqwm8znoo7plhqkc9e5nvkacmtnoafzty4x9md00ol96iaq984o Usqp Cau




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3




X 7 Y 3 5 X 2 Y 9 6 By Elimination Method Novocom Top




Solve For X And Y Linear Equations Using The Elimination Method 2x 6y 2 5x 3y 3 And 9x 3y 5 9x 4y 6 Homeworklib




3 X 1 Y 9 0 2 X 3 Y 5 Mathematics Topperlearning Com G53lykpp




3 X 1 Y 9 And 2 X 3 Y 5 By Elimination Method Brainly In




Q5 10 Points Solve The Equations Using Gauss Chegg Com



Linear Equation In Two Variables System Of Equations




Solve By Elimination Method 1 5 X 2 1 4 1 Y 4 X 2 5 1 Y Maths Linear Inequations Meritnation Com




1 Using The Elimination Method Solve Each Of T Gauthmath




Solve The Following Pair Of Linear Equations By The Elimination M




Example 17 Solve 2 X 3 Y 13 5 X 4 Y 2 Examples




0 0 0 0 6 Solve The System Of Linear Equations Chegg Com



Solve The Following Systems Of Equations 3 X Y 2 X Y 2 9 X Y 4 X Y 1 Sarthaks Econnect Largest Online Education Community




Practice Problems Mat110 Chapter 9




Solve By Elimination Method X 1 2 Y 1 3 9 And X 1 3 Y 1 2 8 Brainly In




Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths




Solve The Following System By Gauss Elimination Method M3 Notes Question Answer Collection




Solve Each With Substitution 2x Y 6 Y 3x 5 3x 4y 4 Y 3x Ppt Download




Asap Please 1 Solve The Following Simultaneous Equations 1 Graphically And Ii Using The Elimination Method Homeworklib




Solve Th 1 Elimination 2x Y 5 3x Y 10 E Chegg Com




Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths




Question Bank Equations Linear Algebra




Exercise 1 5 Matrix Gaussian Elimination Method Problem Questions With Answer Solution




3x Y 3 Justanswer




X 7 Y 3 5 X 2 Y 9 6 By Subsitution Method Brainly In




1 Solve The System Using Substitution Method 2x Y Chegg Com



1
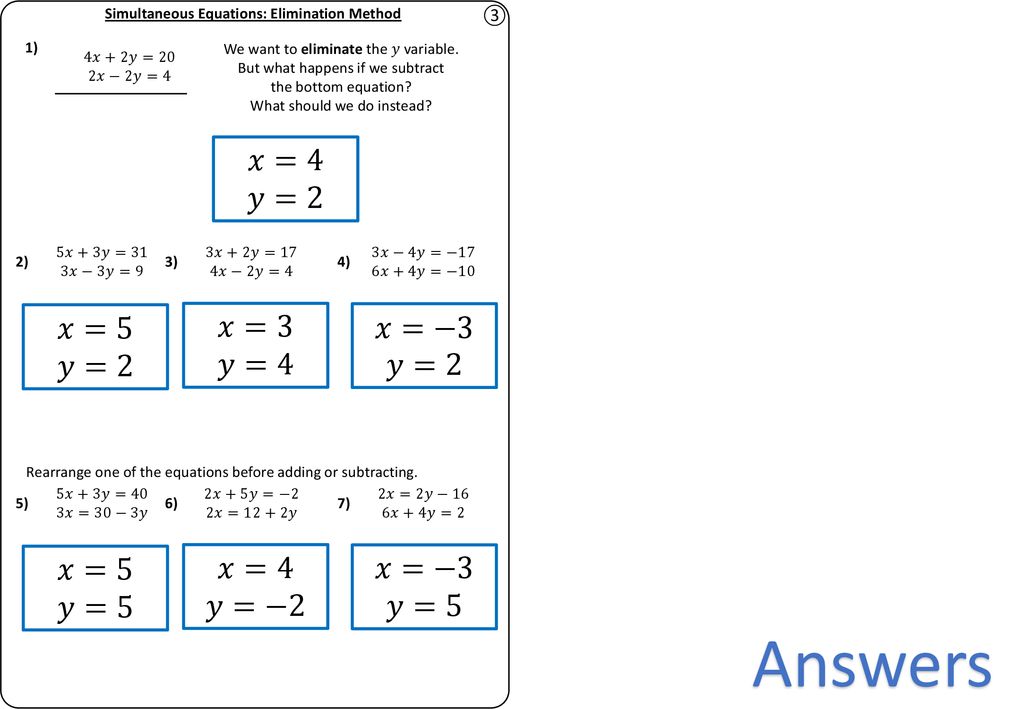



Simultaneous Equations Elimination Complete Lesson Ppt Download
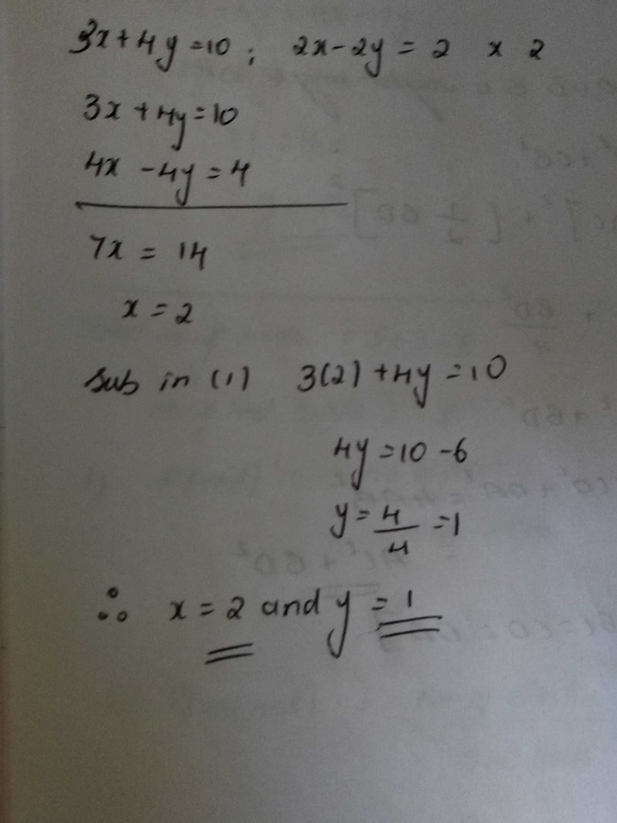



Solve Elimination Method 3x 4y 10 And 2x 2y 2 Scholr




5 41 5 0 6 30 Solve Each System Using Gaussian Chegg Com




Chapter 5 Review Exercises



Q Tbn And9gcrsalf0q4lsed9ius4wevoddfzyytzzmh71v7soscjacjak6vmo Usqp Cau




3 X 1 Y 9 2 X 3 Y 5 Solve Using Elimination Method Mathematics Topperlearning Com T5ibnqll




Exercise 1 5 Matrix Gaussian Elimination Method Problem Questions With Answer Solution




Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Examples




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y




3 Y 7 Cheap Online



Www Ualberta Ca Csproat Homework Math 334 Assignment solutions Assignment 2 solutions Pdf




Ex 4 6 13 Solve Linear Equations Using Matrix Method Ex 4 6




8 Find The Inverse Of A 3 9 Solve The Following Chegg Com




X 2y 1 2x 3y 9 See How To Solve It At Qanda




Simultaneous Equations




Lo I Can Solve Simultaneous Equations Date




By Elimination Method Solve 3 2x 2 3y 5 5 X 3 Y 1 Brainly In




2x Y 2 X 3y 15 By Elimination Method




Homework Lesson 4 Solve Each System Using The Chegg Com




Math 163 Online Problems Supplemental Lessons On Gaussian




Solve 2 X 2 3y 1 6 And 3 X 2 Y 0 And Hence Find A For




7 Solve The Following System Of Linear Equations Chegg Com




X 1 2 Y 1 3 8 X 1 3 Y 1 2 9 Simultaneous Linear Equation Brainly In



Solve The Following Systems Of Equations 2 X 3 Y 2 4 X 9 Y 1 Sarthaks Econnect Largest Online Education Community
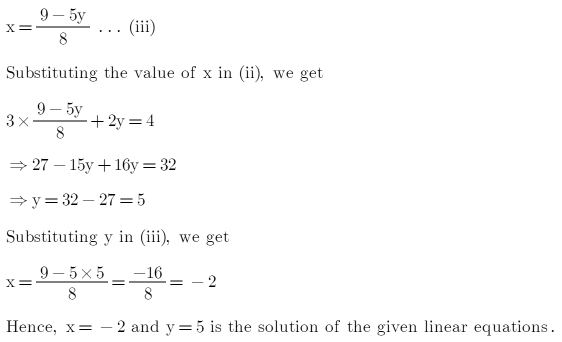



By The Substitution Method Solve The Linear Equation That Is 8 X 5 Y Is Equal To 9 And 3 X 2 Y Is Equal To 4 Mathematics Topperlearning Com Usvpr6ll




Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths




Solve For X And Y X 1 2 Y 1 3 9 And X 1 3 Y 1 2 8 Brainly In




5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Solve These Equations By Elimination Method Maths Pair Of Linear Equations In Two Variables Meritnation Com




How To Solve Simultaneous Equations Using Substitution Method




2 Solve The System With Using Gaussion Chegg Com




2x 3y 9 3x 4y 5 Solve By Elimination Method Brainly In




1 Solve Using The Substitution Method Y 2x 3 Y X 5 Chegg Com




Solving Systems Of Equations Algebraically Substitution Method The




Ex 4 6 13 Solve Linear Equations Using Matrix Method Ex 4 6



0 件のコメント:
コメントを投稿